Matematica del continuo

Equazione differenziale lineare di II° ordine omogenea

Nel caso in cui l'equazione differenziale lineare di II ordine è omogenea avrà il seguente aspetto:

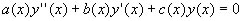
Supponiamo di essere riusciti a trovare due funzioni tra loro indipendenti y₁(x) e y₂(x) che soddisfano l'equazione assegnata allora anche la funzione è soluzione dell'equazione differenziale. Tale proprietà si chiama principio di sovrapposizione. Se y₁(x) è soluzione allora:

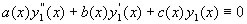
analogamente per y₂(x) avremo:

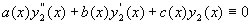
sostituiamo nell'equazione differenziale:

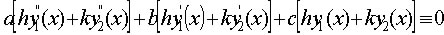
che si può scrivere come:

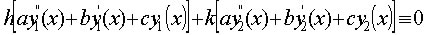
ma i termini in parentesi sono nulli per ipotesi, quindi si ottiene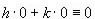

Essendo l'equazione di secondo ordine il problema di Cauchy sarà del tipo:

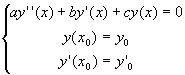
Si tratta di cercare due funzioni y₁(x) e y₂(x) che siano funzionalmente indipendenti e ognuna soluzione dell'equazione differenziale. Le soluzioni si possono cercare tra le funzioni del tipo: 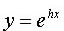che hanno il vantaggio di essere sempre positive. Il nostro problema si riduce a determinare la costante h, a tale scopo costruiamo le seguenti derivate:

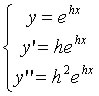
E sostituendole nell'equazione di partenzasi ricava:

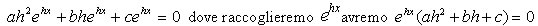
Affinché la quantità precedente sia nulla dovrà essere 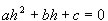, che si chiama equazione caratteristica dell'equazione differenziale. Essendo di secondo grado ammetterà due radici:

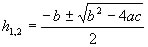
che possono essere:

• Caso 1 - Reali e distinte: h₁ 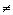h₂ se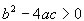

• Caso 2 - Reali e coincidenti: h₁ = h₂ = h se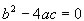

• Caso 3 - Complesse coniugate: h₁ = a + ib e h₂ = a - ib se

Caso 1

L' equazione caratteristica ammette due raidic reali e distinte, in tal caso le due funzioni sono:

che costituisce un sistema di due equazioni nelle due incognit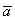e e . Se questo sistema ammette soluzione, allora in questo caso esiste un'unica funzione che soddisfa il problema di Cauchy:

Caso 2

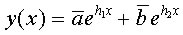
L' equazione caratteristica ammette radici reali e coincidenti In tal caso si trova un solo integrale del tipo:

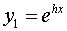
Si dimostra che anche 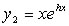è integrale dell'equazione differenziale di partenza ed è funzione indipendente da y₁(x) .

Caso 3

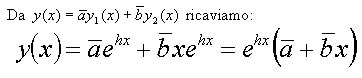
L' equazione caratteristica ammette radici complesse coniugate. Supponiamo siano del tipo h₁ = a + ib e h₂ = a - ib. I due integrali associati hanno la forma:

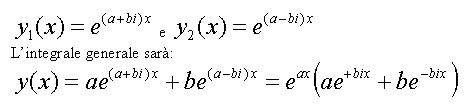
Ricordando la trigonometria complessa osserviamo che la formula di Eulero sui numeri complessi è:

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.