La formula chiave, formula che apre le porte all’insieme di Mandelbrot e porta l’ordine nel caos:
z=z2+c;
Ora rimane il problema di scegliere il valore iniziale di c e z. Una possibilità è dare sempre valore zero a z e scegliere valori diversi per c. Si continua così l’iterazione facendo variare sistematicamente c su una porzione del piano complesso: se il numero complesso fugge verso l’infinito, lo si colora di bianco, in caso contrario di nero. Le pareti di questa prigione virtuale assumono la forma dell’insieme di Mandelbrot. Seguendo invece la regola opposta, in cui teniamo fisso c e z diventa il punto che varia, l’insieme risultante appare assai diverso dall’ insieme di Mandelbrot e viene chiamato insieme di Julia: di questi insiemi ve ne sono a palate; per ciascun valore prefissato di c usato nella formula di iterazione, appare un diverso insieme di Julia insiemi di Julia, dal nome del matematico francese Gaston Julia, il primo nel 1918 ad avere compiuto studi di questo genere mentre si trovava in un ospedale militare, convalescente per le ferite riportate durante la prima guerra mondiale. Quando si applica la formula a un punto iniziale z, la successione risultante, come abbiamo visto, può comportarsi in due modi diversi: può vagare senza limitazioni, allontanandosi verso l’infinito, oppure restare confinata in una certa regione del piano complesso. I punti liberi costituiscono il piano di fuga, mentre quelli che restano confinati formano l’insieme prigioniero. Se il punto di partenza z appartiene all’insieme prigioniero, esso genera una successione interna all’insieme, indipendentemente dal numero di iterazioni e la forma di questa "prigione" dipende solo dal valore di c. L’insieme di Julia separa l’insieme di fuga da quello prigioniero. Scrivendo un programma per visualizzare insiemi di Julia, si può notare che per ogni parametro c, l’immagine risultante è di due tipi: l’insieme può essere un unico insieme connesso, oppure può essere costituito da un numero infinito di punti non connessi e dispersi. Bisogna perciò tenere d’occhio la successione generata dalla solita formula con z=0: se questa successione non diverge verso l’infinito l’insieme di Julia è connesso. Questo avviene in quanto se il punto c scelto è all’interno dell’insieme di Mandelbrot, il corrispondente insieme di Julia risulta connesso, mentre se si sceglie c all’esterno dell’insieme di Mandelbrot, l’insieme di Julia risulterà non connesso. Per scrivere un programma per visionare questi insiemi, si usano certi algoritmi di base. Questi algoritmi hanno in comune il processo iterativo centrale, che dipende da un particolare teorema: se la dimensione di z iterato raggiunge 2, si perde nell’infinito senza possibilità di ritorno. Questo fatto distingue i punti esterni e quelli interni all’insieme. Solitamente si lasciano 100 iterazioni per raggiungere la dimensione 2. Quando invece si deve visionare una parte "zoommata" dell’insieme, invece che con 2, la grandezza di z viene confrontata con 100 o addirittura 1000. Una volta raggiunto 2, la grandezza aumenta molto rapidamente e raggiunge i sopraccitati valori molto velocemente e in poche iterazioni. Le velocità diverse con cui i vari iterati di z superano il valore di soglia, possono essere colorate con colori diversi. È con questa tecnica che si producono le varie e colorate immagini frattali che si vedono in giro, come le seguenti.

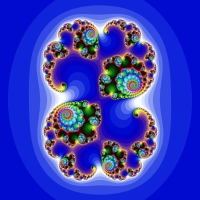

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.