|
|
Sia y = f(x) una funzione continua in un intervallo (a,b) e sia sempre al di sopra dell'ascisse.
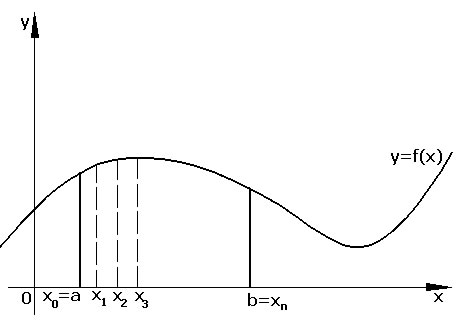
Il problema da risolvere è quello di determinare l'area della
regione compresa tra l'asse x, le due rette di confine y = a e y = b e la funzione
curvilinea. L'idea è di suddividere l'intervallo in sottointervalli di ampiezza
uguale e di costruire dei trapezoidi che hanno tre lati rettilinei ed uno curvilineo.
A partire dal punto a = x0 si arriva al punto b = xn mediante
passi di ampiezza 
arbitrari. Costruiamo
ora, per ogni intervallo, il rettangolo inscritto.
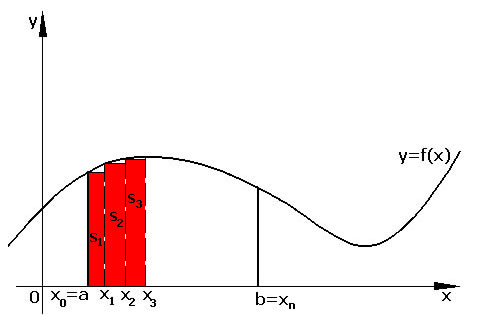
Valutiamo l'area approssimata della regione R in questione: Diciamo S1, S2,----.Sn le aree corrispondenti:
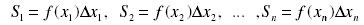
La somma di tali aree approssimerà l'area che volgiamo calcolare:
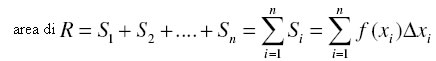
Il valore dell'area si ottiene valutando l'area precedente al tendere di 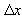i a zero, ossia:
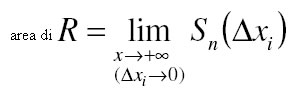
La scrittura precedente significa che all'infittirsi dei punti
di suddivisione dell'intervallo [a,b] il passo della suddivisione deve diventare
piccolissimo (infinitesimo). In termini più rigorosi si definisce la partizione
di un intervallo [a,b] in n sottointervalli arbitrari in cui l'ampiezza dell'iesimo
intervallo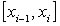 
vale:
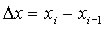
Si chiama norma della partizione e si indica con ||P|| la quantità:
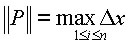
Siccome y = f(x) è continua in tutto l'intervallo, per un noto teorema di Weierstrass, essa assume in ogni sottointervallo valore massimo e minimo.
Teorema di Weierstrass: Se y = f(x) è una funzione continua nell'intervallo chiuso [a,b] e derivabile in (a,b) allora tale funzione assume nell'intervallo valore massimo e minimo. |
Ciò assicura che in ogni intervallo esistono dei numeri reali li e ni tali che:
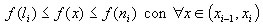
Se f(x) >= 0 nell'intervallo [a,b] allora le quantità f(li)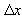i e f(ni)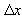i rappresentano
le aree dei rettangoloidi di base 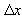i e di lato superiore passante per i punti più
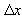alto e più basso del grafico di f(x) nell'intervallo i.
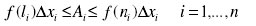
Sia P una partizione di [a,b] si chiama:
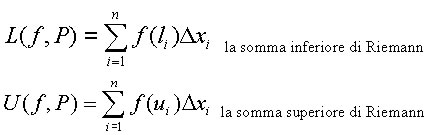
Se infittendo i punti della partizione le somme inferiori e
superiori di Riemann
convergono ad un valore comune, tale valore rappresenta l'area della regione
interessata. Se per ogni partizione esiste un unico numero I tale ch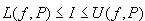e 
allora si dice che y = f(x) è integrabile nell'intervallo
ed I si chiama l'integrale definito
nell'intervallo e si scrive:
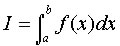
Le quantità a e b si chiamano estremi di integrazione.
La funzione f(x) si chiama funzione integrando.
dx è il differenziale della variabile indipendente x.
Per tutte le possibili partizioni P dell'intervallo [a,b] si ha quindi:
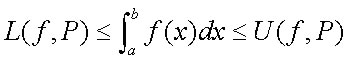
La scrittura precedente vale:
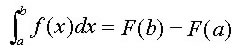
dove F(x) è una primitiva di f(x) (Teorema fondamentale del calcolo integrale).
Di seguito alcuni esempi:
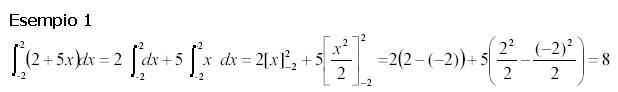
Osservazione: Il calcolo dell'integrale si basa sull'ipotesi che la funzione integrale y = f(x) sia continua in tutti i punti dell'intervallo di integrazione. Pertanto, ai fini del calcolo, bisogna accertarsi che non vi siano punti di discontinuità nell'intervallo di integrazione. Se ad esempio si dovesse calcolare:
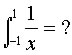
poiché 1/x è discontinua nel punto x = 0 che appartiene all'intervallo di integrazione [-1,1] l'integrale non è risolvibile con le regole viste fin'ora. Un integrale di questo tipo si chiama integrale improprio e va calcolato con tecniche differenti da quelle esposte.
Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.