Il gruppo simmetrico su n oggetti

Consideriamo un insieme X di n >1 elementi
X = {a₁, a₂,..., a_n}
Pensiamo ad ogni permutazione p di X come ad una applicazione biunivoca p : X->X e sia @ la composizione di applicazioni (p₁@ p₂ = p₁(p₂), quindi si applica prima p₂, poi p₁).
L'insieme di tutte le permutazioni (o sostituzioni) di X con l'operazione @ è un gruppo, detto gruppo simmetrico su n oggetti e indicato con Sn. Possiamo indicare gli elementi di Sn in questo modo:

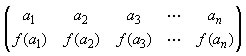
sulla prima riga gli elementi nell'ordine iniziale, sulla seconda gli stessi elementi dopo la permutazione f. La composizione di due permutazioni si ottiene applicando successivamente le due permutazioni

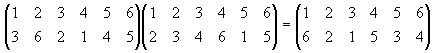
Partendo da destra verso sinistra 1 va in 2, mentre nel primo gruppo 2 va in 6, quindi 1 va in 6; sempre da destra verso sinistra 2 va in 3, mentre nel primo gruppo 3 va in 2, quindi 2 rimane in 2 e cosi via……… L'inversa di una permutazione si ottiene scambiando la prima con la seconda riga la permutazione stessa e poi riordinando gli elementi della prime riga.

In alcune permutazioni succede che un numero m < n di elementi permuti ciclicamente, lasciando fissi gli altri. Una permutazione di questo tipo viene chiamata ciclo di lunghezza m e indicata con:

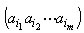
Gli elementi lasciati fissi non vengono usualmente scritti.
Per convenzione, l'identità di S_n viene considerata un ciclo di lunghezza 1.

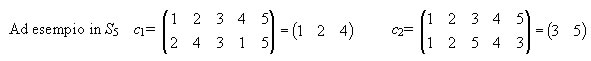
Due cicli c₁ e c₂ di S_n si dicono disgiunti se gli elementi che permutano sono differenti.
TEOREMA. Ogni permutazione può essere scritta come prodotto di cicli disgiunti in modo unico (a meno dell'ordine).

I cicli di lunghezza 2 sono detti trasposizioni o scambi.
TEOREMA. Ogni sostituzione può essere scritta come prodotto di trasposizioni.
ESEMPIO: (1 2 4 6 3) = (1 3)(1 6)(1 4)(1 2)
Tale scrittura non è in generale unica, ma tutte le rappresentazioni di una stessa sostituzione sono costituite da un numero pari o dispari di trasposizioni.
Nel primo caso la sostituzione si dice di classe pari, altrimenti è di classe dispari.
Se una sostituzione è un ciclo, il suo periodo è dato dal numero degli elementi del ciclo stesso.
ESEMPI:
La sostituzione (1 3 5 4) ha periodo 4 infatti le sue potenze sono:
(1 3 5 4), (1 3 5 4)² = (1 5)(3 4), (1 3 5 4)³ = (1 4 5 3), (1 3 5 4)⁴ = id.
Se una sostituzione è un prodotto di cicli disgiunti, il suo periodo è dato dal minimo comune multiplo tra i periodi dei vari cicli.

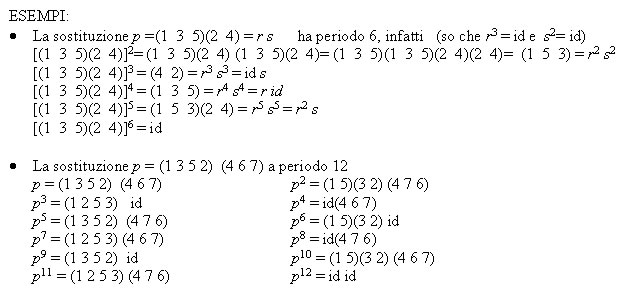
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.