DEFINIZIONE. Se un sottoinsieme S di un gruppo (A, @) è a
sua volta un gruppo rispetto alla stessa operazione definita in A, allora si
dice che S è un sottogruppo di (A, @).
sottogruppi impropri o banali: ci sono per ogni gruppo e sono due:
{elemento neutro} e A;
sottogruppi propri gli altri, se esistono.
Condizione NECESSARIA ma non sufficiente perché un sottoinsieme S di (A,@) sia
sottogruppo è che contenga il neutro di A. Questa proprietà serve a verificare
che in qualche caso un sottoinsieme NON è un sottogruppo. Ma non essendo sufficiente
se un sottoinsieme contiene il neutro non è detto che sia un sottogruppo. Non
serve comunque verificare tutti gli assiomi: basta il
CRITERIO: Sia S un sottoinsieme del gruppo (A, @). (S, @) è un sottogruppo se
e solo se per ogni coppia a, b di elementi di S risulta a @ b-1 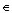 S. Se il gruppo
S ha ordine finito, basta verificare che sia a @ b
S. Se il gruppo
S ha ordine finito, basta verificare che sia a @ b 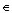 S
S
Si possono ottenere alcuni sottogruppi di un gruppo qualsiasi (A, @) nel modo
seguente: preso un elemento a di A, l'insieme di tutte le potenze di a in A
è un sottogruppo di A.
Consideriamo i gruppi (Zn,+). Dalle tavole pitagoriche:
In Z5 non ci sono sottogruppi propri.
In Z6 si verifica che {0,2,4} e {0,3} sono due sottogruppi.
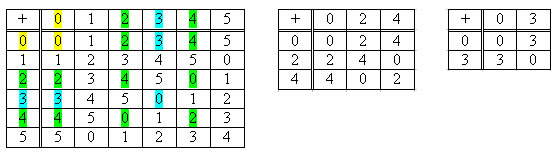
Si può notare che se n è primo (Zn,+) non contiene sottogruppi,
se n è composto, contiene come sottogruppi quelli formati dai multipli di un
suo divisore qualsiasi. Vale infatti il fondamentale:
TEOREMA DI LAGRANGE. L'ordine r di un sottogruppo B di un gruppo finito (A,
@) è un divisore dell'ordine n di A.
Una immediata conseguenza del teorema di Lagrange è che se un gruppo ha un numero
p primo di elementi, non ammette sottogruppi propri.
Esempi:
Gli elementi del sottogruppo A di S6 generato da a = (1 4 2 6 5
3) sono:
A ={a, a2, a3, a4, a5, a6=id}=
{(1 4 2 6 5 3), (1 2 5)(3 4 6), (1 6) (2 3) (4 5) , (1 5 2)(3 6 4), (1 3 5
6 2 4), id}
Consideriamo (Z*12,x) = {1, 5, 7, 11}. Cerchiamo i sottogruppi.
Calcoliamo il periodo degli elementi di (Z*12,x)
Periodo di 5 52 ![]() 1
mod 12 -> è 2 quindi {1, 5} è sottogruppo di (Z*12,x)
1
mod 12 -> è 2 quindi {1, 5} è sottogruppo di (Z*12,x)
Periodo di 7 72 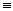 1 mod 12 -> è 2 quindi {1,
7} è sottogruppo di (Z*12,x)
1 mod 12 -> è 2 quindi {1,
7} è sottogruppo di (Z*12,x)
Periodo di 11 112 ![]() 1 mod 12 -> è 2 quindi {1, 11} è sottogruppo di (Z*12,x)
1 mod 12 -> è 2 quindi {1, 11} è sottogruppo di (Z*12,x)
Non ne esistono altri, in quanto gli ordini possibili dei sottogruppi sono
solo 1, 2, 4 (il gruppo è di ordine 4). I sottogruppi di ordine 1 o 4 sono
impropri e di ordine 2 non ne possono esistere altri: devono contenere solo
l'identità e un elemento, e quindi sono solo quelli.
Consideriamo (Z*16,×) = {1, 3, 5, 7, 9,11, 13, 15}. Cerchiamo i sottogruppi.
Z*16 ha ordine 8. I divisori di 8 sono 1, 2, 4, 8.
1 {1}
3 {3, 9, 11, 1}
5 {5, 9, 13, 1}
7 {7, 1}
9 {9, 1}
11 {11, 9, 3, 1}
13 {13, 9, 5, 1}
15 {15, 1}
Questi potrebbero non essere tutti i sottogruppi generati dagli elementi.
Ci sono elementi di periodo 2 che potrebbero essere contenuti in sottogruppi
propri di ordine 4: proviamo a costruire il sottogruppo che contiene 7 e 9…
deve contenere anche 72, 92e 7×9, quindi {7, 9, 1, 15} non generato da nessun
elemento.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.